Artificial Intelligence
A Brief Introduction to Game Theory: The MiniMax Algorithm
Breaking Down Non co-operative Game Theory
By definition, game theory is "the study of mathematical models of conflict and cooperation between intelligent rational decision-maker"1. Where a rational decision-maker is someone who is trying to maximize their rewards. Non co-operative game theory implies that players work independently and are not assuming what the other player is doing2.
What is the MiniMax Algorithm
The MiniMax algorithm is one approach to computing the best possible outcome by recursively generating all possible final states of a game(which can be represented as a tree, where the final states are the leaf nodes) while simultaneously keeping track of the current optimal node and comparing that to all other siblings of that node. Before exploring my example below we will need to make a few assumptions.
1.) Each level of the tree alternates between each players turn.
Figure 1: Visual representation of each players turn
2.)
- 1 = player 1 wins
- 0 = tie
- -1 = player 2 wins
3.) We are running the algorithm as the optimal strategy for player one. Therefore, If it is player 1's turn, they will choose the next state with the highest return. Alternatively, if it is player 2's turn, we will assume that they will always pick the next state with the lowest return. This is because we are running the algorithm for player 1 and the state with the lowest return is equal to the state with the highest return for the other player.
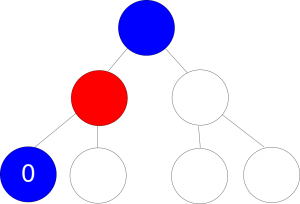
Figure 2: Path leads to tie
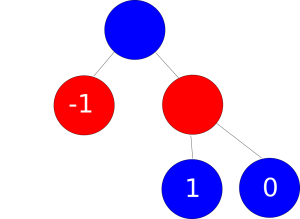
Figure 3: Path leads to loss
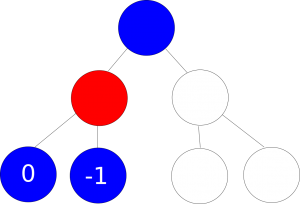
Figure 4: Player 2 chooses the lowest number
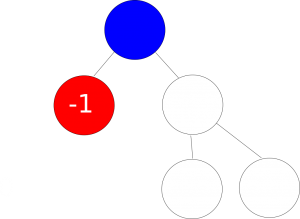
Figure 5: Path leads to a win
Figure 6: Path leads to a tie
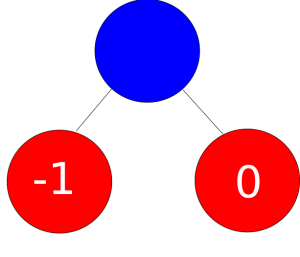
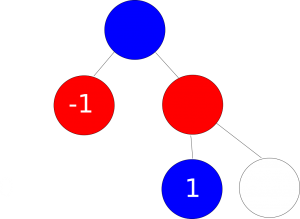
Figure 7: Player 2 picks the state with the lowest number
Figure 8: Tie game: Player 1 picks the state with the highest number
Following the example images above if player 1 and player 2 both follow the optimal strategy, he/she can only tie at best. In other words this is considered a zero sum game. Of course, this result will only occur if both players are using the optimal strategy.
Pseudocode
function miniMax(board, player) {
if (player1) {
highestReturn = -2
for each possible move on the board {
board = makeMove(board)
result = miniMax (board, player2)
highestReturn = max(highestReturn, result)
}
return highestReturn
else { // player2
lowestReturn = 2
for each possible move on the board {
board = makeMove(board)
result = miniMax (board, player1)
lowestReturn = min(highestReturn, result)
}
return lowestReturn
A Brief High Level Analysis of the Algorithm
We can quickly analysis the pseudocode above by breaking it down. Although we did not define the min(), max(), and makeMove() functions we can assume that these functions have a constant runtime, or O(1). Therefore, they will not have an affect on the overall runtime of our miniMax algorithm. To analysis the runtime of this algorithm, we will take a look at the binary tree.There are two factors that will affect the big-oh notation of our runtime, the number of possible moves at each node and the depth of our binary tree. In this case at each node a player has 2 possible options and our tree has a depth of 3. This makes our runtime O(23-1). We can simplify this to O(23). Finally we can say for any game, the runtime of our miniMax algorithm is O(nm), where n is equal to the number of moves per node and m is equal to the number of levels in our tree. As you can probably tell, this algorithm grows very quickly
Wrapping Up
Although, the miniMax algorithms computes the optimal strategy it is important to note that it has an extremely large big-oh bound. This wouldn't necessarily be an issue for games with relatively few possible states such as tic tac toe, but it certainly becomes an issue with games that have numerous possible states. For games with many possible states, like chess, it is important to optimize this algorithm by either adding a heuristic or stopping the recursive calls after a certain number of moves. This is often done by using a technique called alpha-beta pruning.
References
1.) Myerson, Roger B. (1991). Game Theory: Analysis of Conflict, Harvard University Press, p. 1. Chapter-preview links, pp. vii–xi.
2.) Department of Computer Science and Engineering, IIT Delhi. N.p., n.d. Web. 07 Dec. 2016, https://www.cse.iitd.ernet.in/~rahul/cs905/lecture1.html.
